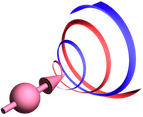Light is usually pictured as waves with plane wavefronts. It turns out (for coherent sources as lasers) that this is the exception: Most of the time, lots of information is contained in the phase structure. One basis in which one can describe this structure are the Laguerre-Gaussian modes. In general, their wavefronts are fusili-shaped, or “twisted”. In 1992 it was found that this light carries true orbital angular momentum (OAM), this discovery started a completely new field. In my opinion, one reason is, that the concept of optical OAM gives an intuitive understanding of the usually very complex “spatial structure of light”.

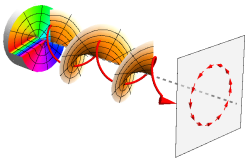
A twisted-light beam can be produced by sending a plane-wave beam through a spiral phase plate (left). The arrow sketches the local momentum, which adds up to the total OAM of the beam.

Higher-order optical vortices are inherently unstable in the sense that they tend to split up in a series of vortices with unity charge. We demonstrate this vortex-splitting phenomenon in beams produced with holograms and spatial light modulators and discuss its generic and practically unavoidable nature. The picture shows a microscopic view into the core of a charge-3 vortex. To analyse the splitting phenomena in detail, we use a multi-pinhole interferometer to map the combined amplitude and phase profile of the optical field.

Instability of higher-order optical vortices analyzed with a multi-pinhole interferometer, Opt. Express 20, 22961 (2012)

An ideal mirror has Fresnel reflection coefficients which are either 1 or -1. In reality, this does of course not exist, and diffractive corrections occur. We have found that these lead to a modification of the OAM spectrum of a reflected beam, and that the modifications increase with decreasing reflectivity of the interface. We developed a theory which introduces the spatial Fresnel coefficients, an analogy of Fresnel's polarization coefficients in transverse-mode space. With this theory, one can calculate how optical modes are modified upon reflection, for any planar interface.

Observation of OAM sidebands due to optical reflection, Phys. Rev. Lett. 109, 113602 (2012)
preprint: http://arxiv.org/abs/1204.4003

As a first step (and to contribute to an ongoing discussion), we asked ourselves if the circular dichroism of a cholesteric polymer (a solid form of a cholesteric liquid crystal) is sensitive to the light's twist under strong-focussing condition. The latter point makes this in particular interesting, because in focussed light beams, the spin (polarization) couples to the orbital (phase) angular momentum.

In this publication we set new bounds for such a possible interaction:
Phys. Rev. A 83, 065801 (2011) http://arxiv.org/abs/1104.0556: Circular dichroism of cholesteric polymers and the orbital angular momentum of light

With this we also demonstrate, for the first time experimentally, that spin-orbit coupling in optics is not a two-way street as it is in solid-state physics and that this term should be used with caution.

How is twisted light scattered by helical particles? The interesting case is that of very small particles, let's say, of the order of a few optical wavelengths. Clearly, the twisted light, which we scatter from such particles, has to be focussed strongly, and this regime is not well known.

Helical particles (left) appear often in nature: Many building blocks, i.e., molecules, are chiral, and self-assembly frequently leads to a helical super-structure. Twisted light (right) is light with helical wavefronts.